Isentropic Vortex in 2D
This example is taken from Spiegel et al. (2015), namely Section IV.A.1. Hence, the exact solution is based on the Gaussian pulse
\[\Omega = \beta e^{f},\]
where \(f(x,y) = -\frac{1}{2\sigma^2} \Big( r^2/ R^2 \Big)\), with \(r^2 = (x-x_c)^2 + (y-y_c)^2\) and \((x_c, y_c)\) corresponds to the initial location of the pulse. Using this function, we define the perturbations to the velocity and temperature as
\[\delta u = - \big( y/R \big) \Omega, \qquad
\delta v = \big( x/R \big) \Omega, \qquad
\delta T = - \big( \overline{\gamma}/2 \big) \Omega^2,\]
with \(\overline{\gamma} = \gamma - 1\) and the specific heat ratio is taken as \(\gamma = 1.4\).
Afterwards, these perturbations along with an isentropic flow assumption (\(\delta s = 0\), where \(s = p/\rho^\gamma\)), we generate the analytic solution. In primitive variables, this reads
\[\rho = \big( 1 + \delta T\big)^{1/\overline{\gamma}},\qquad
u = M_\infty \cos \alpha + \delta u,\qquad
v = M_\infty \sin \alpha + \delta v,\qquad
p = \rho^{\gamma}/\gamma,\]
where \(M_\infty\) is the mean Mach number and \(\alpha\) is the flow angle, taken with respect to the \(x\)-axis.
Following d’Alembert’s solution, the above analytic solution at any given time is simply the shift of the initial condition (\(t = t_0\)). This can be represented by substituting the initial coordinates \(x\) and \(y\) with
\[x(t) = x - u_\infty t,\qquad
y(t) = y - v_\infty t,\]
where \((u_\infty, v_\infty)\) is the mean velocity, obtained from the Mach number and flow direction via \(u_\infty = M_\infty \cos \alpha\) and \(v_\infty = M_\infty \sin \alpha\).
For this specific example, the parameters used are: a mean Mach number of \(M_\infty = 0.5\), a Gaussian amplitude of \(\beta = M_\infty \frac{5 \sqrt{2}}{4 \pi} e^{1/2}\) with a characteristic width of \(R = 1\), a flow angle of \(\alpha = 45^{\circ}\) on a grid \(\boldsymbol{x} \in [-5,+5]^2\) with an initial pulse center situated at \((x_c, y_c) = (0, 0)\). The total duration of this simulation is taken as \(t \in [0,5]\). Note, all variables are non-dimensional, by definition.
[1] Spiegel, Seth C., H. T. Huynh, and James R. DeBonis.
“A Survey of the Isentropic Euler Vortex Problem Using High-Order Methods.”
22nd AIAA Computational Fluid Dynamics Conference, 2015.
[1]:
# Import preliminary modules.
from dream import *
from dream.compressible import Initial, CompressibleFlowSolver, flowfields
import ngsolve as ngs
[2]:
# Define the grid.
from netgen.occ import OCCGeometry, WorkPlane
from netgen.meshing import IdentificationType
def CreateSimpleGrid(ne, lx, ly):
# Select a common element size.
h0 = min( lx, ly )/float(ne)
# Generate a simple rectangular geometry.
domain = WorkPlane().RectangleC(lx, ly).Face()
# Assign the name of the internal solution in the domain.
domain.name = 'internal'
# For convenience, extract and name each of the edges consistently.
bottom = domain.edges[0]; bottom.name = 'bottom'
right = domain.edges[1]; right.name = 'right'
top = domain.edges[2]; top.name = 'top'
left = domain.edges[3]; left.name = 'left'
# Pair the boundaries in each direction: vertical and horizontal.
bottom.Identify(top, "ydir", IdentificationType.PERIODIC)
right.Identify(left, "xdir", IdentificationType.PERIODIC)
# Initialize a rectangular 2D geometry.
geo = OCCGeometry(domain, dim=2)
# Discretize the domain.
mesh = ngs.Mesh(geo.GenerateMesh(maxh=h0, quad_dominated=True))
# Return our fancy grid.
return mesh
[3]:
# Generate the grid.
# Number of elements per dimension.
ne = 10
# Dimension of the rectangular domain.
lx = 10.0
ly = 10.0
# Generate a simple grid.
mesh = CreateSimpleGrid(ne, lx, ly)
# Message output detail from netgen.
ngs.ngsglobals.msg_level = 0
ngs.SetNumThreads(4)
[4]:
# Class containing all the parameters to define an isentropic vortex.
class IsentropicVortexParam:
def __init__(self, cfg):
# Center of the vortex, assumed at the center of the domain.
# Currently, this assumes that the domain is: [0,lx],[0,ly].
self.x0 = 0.0
self.y0 = 0.0
# Vortex parameters, found in Spiegel et al. (2015).
self.theta = 45.0 # flow angle [deg].
self.Tinf = 1.0 # background temperature.
self.Pinf = 1.0 # background pressure.
self.Rinf = 1.0 # background density.
self.Minf = 0.5 # background Mach.
self.sigma = 1.0 # Perturbation strength.
self.Rv = 1.0 # Perturbation width.
# Scaling for the maximum strength of the perturbation.
self.beta = self.Minf*ngs.exp(0.5)*5.0*ngs.sqrt(2.0)/(4.0*ngs.pi)
# Convert the angle from degrees to radians.
self.theta *= ngs.pi/180.0
# Deduce the background mean velocity.
self.uinf = self.Minf*ngs.cos( self.theta )
self.vinf = self.Minf*ngs.sin( self.theta )
# Store gamma here, so we do not pass it around constantly.
self.gamma = cfg.equation_of_state.heat_capacity_ratio
# Function that defines the analytic solution.
def InitialCondition(cfg):
# Extract the starting time.
t0 = cfg.time.timer.interval[0]
# Return the analytic solution at time: t0.
return AnalyticSolution(cfg, t0)
# Function that creates a time-dependant analytic solution.
def AnalyticSolution(cfg, t):
# Extract the vortex parameters.
vparam = IsentropicVortexParam(cfg)
# Generate an array of 4x3 vortices. If you need something different, modify it.
# NOTE, in this case, the 4x3 array of vortices assumes:
# 1) flow aligned in (+ve) x-direction.
# 2) simulation is done for only 1 period: tf = lx/uInf.
fn = ngs.CF(())
for i in range(-2,2):
for j in range(-1,2):
fn += GeneratePerturbation(vparam, t, i, j)
# For convenience, extract the perturbations explicitly.
dT = fn[0]; du = fn[1]; dv = fn[2]
# Extract the required parameters to construct the actual variables.
gamma = vparam.gamma
uinf = vparam.uinf
vinf = vparam.vinf
# Abbreviations involving gamma.
gm1 = gamma - 1.0
ovg = 1.0/gamma
ovgm1 = 1.0/gm1
govgm1 = gamma*ovgm1
# Define the primitive variables, by superimposing the perturbations on a background state.
r = (1.0 + dT)**ovgm1
u = uinf + du
v = vinf + dv
p = ovg*(1.0 + dT)**govgm1
# Return the analytic expression of the vortex.
return flowfields( rho=r, u=(u, v), p=p )
# Function that generates a single isentropic perturbations in the velocity and temperature.
# Here, (ni,nj) are the integers for the multiple of (lx,ly)
# distances between the leading/trailing vortices.
def GeneratePerturbation(vparam, t, ni, nj):
# For convenience, extract the information of the vortex.
theta = vparam.theta
Tinf = vparam.Tinf
Pinf = vparam.Pinf
Rinf = vparam.Rinf
Minf = vparam.Minf
sigma = vparam.sigma
Rv = vparam.Rv
beta = vparam.beta
gamma = vparam.gamma
x0 = vparam.x0
y0 = vparam.y0
uinf = vparam.uinf
vinf = vparam.vinf
# Center of the pulse.
xc = x0 + ni*lx
yc = y0 + nj*ly
# Time-dependent pulse center.
xt = (ngs.x-xc) - uinf*t
yt = (ngs.y-yc) - vinf*t
# Abbreviations involving gamma.
gm1 = gamma - 1.0
ovg = 1.0/gamma
ovgm1 = 1.0/gm1
govgm1 = gamma*ovgm1
ovs2 = 1.0/(sigma*sigma)
# The Gaussian perturbation function.
ovRv = 1.0/Rv
f = -0.5*ovs2*( (xt/Rv)**2 + (yt/Rv)**2 )
Omega = beta*ngs.exp(f)
# Velocity and temperature perturbations.
du = -ovRv*yt*Omega
dv = ovRv*xt*Omega
dT = -0.5*gm1*Omega**2
# Return the Perturbations.
return ngs.CF( (dT, du, dv) )
[5]:
# Solver configuration: Compressible (inviscid) flow.
cfg = CompressibleFlowSolver(mesh)
cfg.time = "transient"
cfg.time.timer.interval = (0.0, 5.0)
cfg.time.timer.step = 0.25
cfg.dynamic_viscosity = "inviscid"
cfg.equation_of_state = "ideal"
cfg.equation_of_state.heat_capacity_ratio = 1.4
cfg.scaling = "acoustic"
cfg.mach_number = 0.0
cfg.riemann_solver = "lax_friedrich"
cfg.fem = "conservative_hdg"
cfg.fem.order = 0
cfg.fem.scheme = "implicit_euler"
cfg.fem.solver = "direct"
cfg.fem.solver.method = "newton"
cfg.fem.solver.method.damping_factor = 1
cfg.fem.solver.method.max_iterations = 10
cfg.fem.solver.method.convergence_criterion = 1e-10
Uic = InitialCondition(cfg)
cfg.bcs['left|right'] = "periodic"
cfg.bcs['top|bottom'] = "periodic"
cfg.dcs['internal'] = Initial(fields=Uic)
[6]:
# Decorator for the actual simulation.
import numpy as np
# Extract time configuration.
t0, tf = cfg.time.timer.interval
dt = cfg.time.timer.step.Get()
nt = int(round((tf - t0) / dt))
# Abbreviations.
gamma = cfg.equation_of_state.heat_capacity_ratio
# Define a decorator for the isentropic vortex routine.
def isentropic_vortex_routine(label):
def decorator(func):
def wrapper(*args, draw_solution=False, **kwargs):
# Insert options here.
func(*args, **kwargs)
cfg.fem.order = 4
# Allocate the necessary data.
cfg.initialize()
# Get a reference to the numerical solution and the analytic solution.
uh = cfg.get_solution_fields('rho_u')
ue = AnalyticSolution(cfg, cfg.time.timer.t)
if draw_solution:
# cfg.io.draw({"Density": uh.rho})
# cfg.io.draw({"Mach": cfg.get_local_mach_number(uh)})
# cfg.io.draw({"Exact[Density]": ue.rho})
isentropic_deviation = (uh.p/ue.p) * (ue.rho/uh.rho)**gamma - 1.0
cfg.io.draw({"Deviation[Isentropy]": isentropic_deviation}, min=-0.0001, max=0.0001)
#cfg.io.draw({"Diff[Density]": (ue.rho - uh.rho)}, min=-0.1, max=0.1)
# NOTE, uncomment if you want the norm based on magnitude of the momentum.
mag_rhou_e = ue.rho * ngs.sqrt( ngs.InnerProduct(ue.u, ue.u) )
mag_rhou_n = ngs.sqrt( ngs.InnerProduct(uh.rho_u, uh.rho_u) )
# Integration order (for post-processing).
qorder = 10
# Data for book-keeping information.
data = np.zeros((nt, 3), dtype=float)
with ngs.TaskManager():
# Time integration loop (actual simulation).
for i, t in enumerate(cfg.time.start_solution_routine(True)):
# Compute the L2-norm of the error.
err_rho = np.sqrt( ngs.Integrate( (ue.rho-uh.rho)**2, mesh, order=qorder) )
err_mom = np.sqrt( ngs.Integrate( (mag_rhou_e-mag_rhou_n)**2, mesh, order=qorder) )
# Store data: time and error metrics.
data[i] = [cfg.time.timer.t.Get(), err_rho, err_mom]
return data
wrapper.label = label
return wrapper
return decorator
[7]:
# Specialized routines.
@isentropic_vortex_routine("implicit_euler(hdg)")
def implicit_euler_hdg():
cfg.fem = "conservative_hdg"
cfg.fem.scheme = "implicit_euler"
@isentropic_vortex_routine("bdf2(hdg)")
def bdf2_hdg():
cfg.fem = "conservative_hdg"
cfg.fem.scheme = "bdf2"
@isentropic_vortex_routine("sdirk22(hdg)")
def sdirk22_hdg():
cfg.fem = "conservative_hdg"
cfg.fem.scheme = "sdirk22"
@isentropic_vortex_routine("sdirk33(hdg)")
def sdirk33_hdg():
cfg.fem = "conservative_hdg"
cfg.fem.scheme = "sdirk33"
@isentropic_vortex_routine("imex_rk_ars443(dg)")
def imex_rk_ars443_dg():
cfg.fem = "conservative_dg"
cfg.fem.scheme = "imex_rk_ars443"
@isentropic_vortex_routine("ssprk3(dg)")
def ssprk3_dg():
cfg.fem = "conservative_dg"
cfg.fem.scheme = "ssprk3"
@isentropic_vortex_routine("crk4(dg)")
def crk4_dg():
cfg.fem = "conservative_dg"
cfg.fem.scheme = "crk4"
@isentropic_vortex_routine("explicit_euler(dg)")
def explicit_euler_dg():
cfg.fem = "conservative_dg"
cfg.fem.scheme = "explicit_euler"
[8]:
# Figure style and properties.
from matplotlib import pyplot as plt
# Assign colors to base method names
method_colors = {
"implicit_euler": "tab:red",
"bdf2": "tab:blue",
"sdirk22": "tab:green",
"sdirk33": "tab:purple"
}
# Helper function that sets up a generic figure.
def setup_fig(xlabel, ylabel, title):
fig, ax = plt.subplots(figsize=(15, 6))
ax.set_xlim(t0, tf)
ax.tick_params(axis='both', labelsize=16)
ax.set_xlabel(xlabel, fontsize=14)
ax.set_ylabel(ylabel, fontsize=16)
ax.set_title(title, fontsize=16)
ax.grid(True)
return fig,ax
# Helper function that specifies the plot style properties.
def get_plot_style(label, method_colors):
if label.endswith("(hdg)"):
base_name = label.replace("(hdg)", "").strip()
linestyle = "-"
marker = 'o'
elif label.endswith("(dg)"):
base_name = label.replace("(dg)", "").strip()
linestyle = "--"
marker = '^'
else:
base_name = label.strip()
linestyle = ":"
marker = '.'
color = method_colors.get(base_name, "black")
return {
"label": label,
"linestyle": linestyle,
"marker": marker,
"markersize": 8,
"markevery": 50,
"color": color
}
[9]:
# Run simulation(s).
routines = [implicit_euler_hdg, bdf2_hdg, sdirk33_hdg]
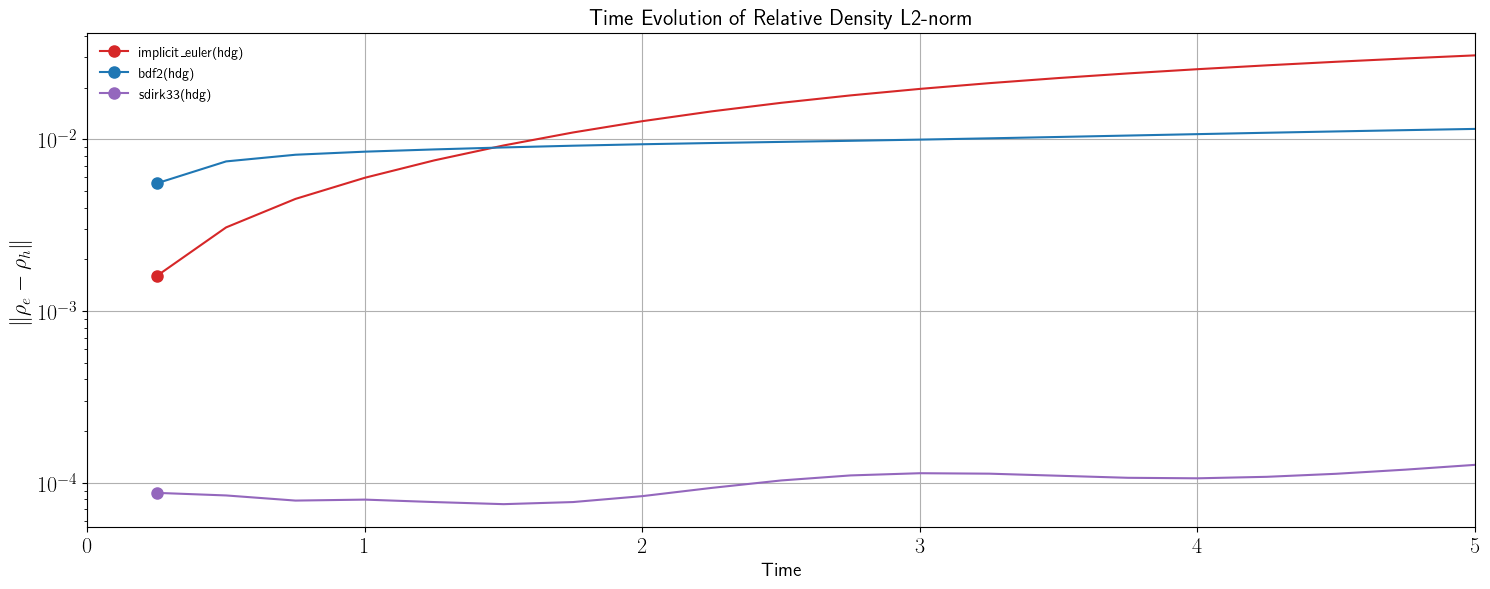
# Figure 1: logarithmic plot of the relative error in the L2-norm: density.
fig1, ax1 = setup_fig("Time", r"$\| \rho_e - \rho_h \|$", r"Time Evolution of Relative Density L2-norm")
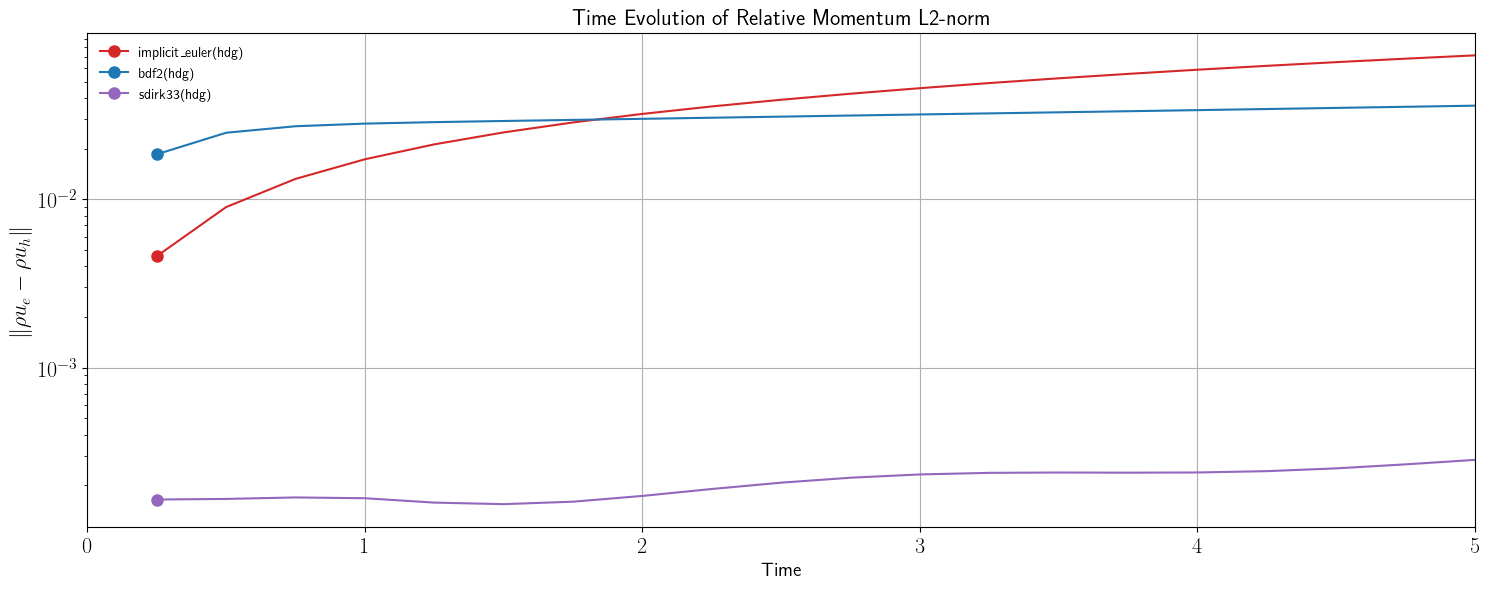
# Figure 2: logarithmic plot of the relative error in the L2-norm: magnitude of momentum.
fig2, ax2 = setup_fig("Time", r"$\| \rho u_e - \rho u_h \|$", r"Time Evolution of Relative Momentum L2-norm")
# Run each simulation.
for routine in routines:
print(f"Running {routine.label}...")
data = routine(draw_solution=False)
style = get_plot_style(routine.label, method_colors)
ax1.semilogy(data[:, 0], data[:, 1], **style)
ax2.semilogy(data[:, 0], data[:, 2], **style)
uh = cfg.get_solution_fields('rho_u')
ue = AnalyticSolution(cfg, cfg.time.timer.t)
isentropic_deviation = (uh.p/ue.p) * (ue.rho/uh.rho)**gamma - 1.0
cfg.io.draw({"Deviation[Isentropy]": isentropic_deviation}, min=-0.0001, max=0.0001)
# Final touches.
ax1.legend(loc="upper left", frameon=False)
ax2.legend(loc="upper left", frameon=False)
fig1.tight_layout()
fig2.tight_layout()
plt.show()
Running implicit_euler(hdg)...
dream.time (INFO) | conservative_hdg implicit_euler | it: 2 | error: 4.068907e-15 | t: 5.00
Running bdf2(hdg)...
dream.time (INFO) | conservative_hdg bdf2 | it: 2 | error: 9.312217e-15 | t: 5.00
Running sdirk33(hdg)...
dream.time (INFO) | conservative_hdg sdirk33 | it: 1 | error: 8.601520e-09 | stage: 3 | t: 5.00
